Profitez de notre cadeau de fin d’année :
10% de réduction sur notre catalogue !
Valable du 10 au 31 décembre 2024.
Avec le code : KDO2024

Mathématiques
Les mathématiques, c’est logique et compréhensible par tous.
Découvrez nos outils pour apprendre avec moins de difficultés !

Pédagogie
Un apprentissage de qualité ? Oui mais pas sans gestion de classe efficace !
Découvrez tous nos conseils et nos principes pour répondre à vos besoins

Français
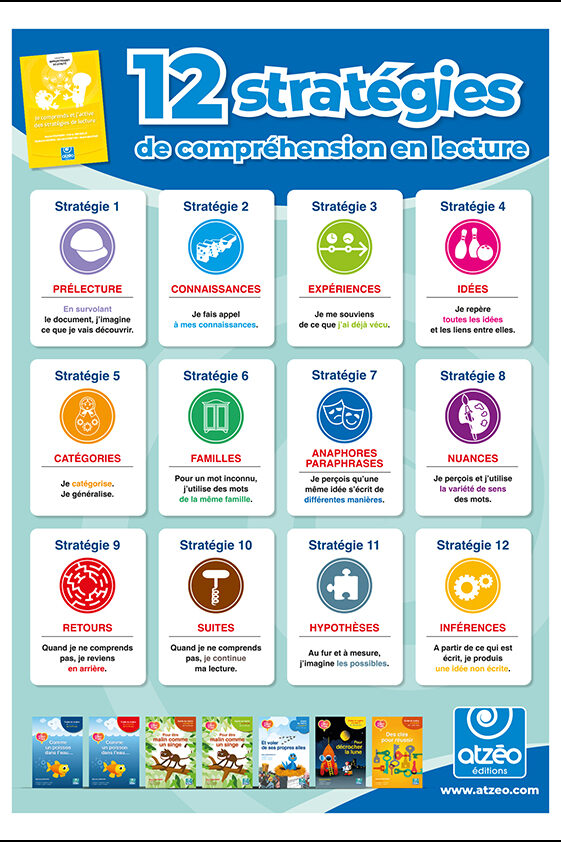
Apprendre VRAIMENT à lire et à écrire !
Chez Atzeo, on dit oui ! Découvrez des stratégies dans nos collections « OhOh » et « Au coeur du lire ».
Téléchargements gratuits
Les actualités des éditions Atzéo
Les éditions pédagogiques Atzéo
La maison d’édition Atzéo édite des livres pédagogiques pour les enseignants et des manuels scolaires pour les élèves. Le public cible est le monde scolaire élargi : enseignants, étudiants en Hautes Ecoles, formateurs, logopèdes, orthopédagogues…
Obstinément au service de l’apprentissage
La ligne éditoriale est tournée sur l’apprentissage de chacun dans une logique collective. C’est pourquoi nos livres scolaires évitent les stéréotypes de genre (ou culturels) et permettent aussi d’assurer un soutien scolaire. Nous abordons de manière professionnelle (fondée sur les neurosciences) les savoirs à mettre en mémoire à long terme. Notre souci d’égalité est mis en application par une pédagogie différenciée sous forme de séquences car il s’agit que chaque élève soit porté au plus haut de ses capacités. Ainsi, des activités de 2e primaire sont aussi parfois utiles pour des élèves de 5e primaire. Le niveau est élevé mais il n’est jamais attendu que les élèves réussissent l’entièreté de la proposition pédagogique.
Nous tenons compte au maximum des référentiels du Ministère de l’éducation (nouveaux programmes) même si nous nous démarquons en visant l’essentiel !
Les collections et manuels des éditions Atzéo
Nos principales collections fournissent aux institutrices et instituteurs :
- des ouvrages scolaires au service de l’apprentissage du français : orthographe et lecture ;
- des ressources pédagogiques pour la construction d’images mentales en maths ;
- des livres pédagogiques avec de nombreuses ressources concrètes.
Pour chaque ouvrage, des documents numériques sont téléchargeables sur le site www.atzeo.com.
Toutes nos productions sont cohérentes les unes avec les autres car notre projet est pédagogique avant d’être commercial. Nous souhaitons proposer des livres et manuels de qualité et donc nous soignons la mise en page et les illustrations en étant attentifs à ce que ces éléments ne distraient pas l’élève de son but d’apprentissage.
De nombreux établissements scolaires ont compris l’intérêt d’utiliser nos collections pour construire une continuité dans leur établissement. Notamment pour l’apprentissage de la lecture (la compréhension écrite) et pour l’apprentissage du savoir écrire.
Des formateurs « experts » apprécient nos nouveautés car elles apportent une pédagogie vivante et interactive. Notre façon d’aborder les matières (dans une logique de compétences) permet de valider les recherches en éducation et les écrits des pédagogues reconnus.
Où trouver nos ouvrages pédagogiques et manuels scolaires ?
En tant qu’éditeur scolaire, nous sommes distribués par des libraires en Belgique et par deux diffuseurs en France. Nous assurons aussi le suivi des commandes directes par internet en interaction avec la Poste.
Le sourire affiché par les élèves en fin de parcours, après avoir vaincu les difficultés, est notre plus beau cadeau.