Différencier avec le calcul’AS 3D

Kersten B.

Instituteur primaire – Directeur d’une école fondamentale

Master en Sciences de l’Education – Co-créateur des calcul’AS 3D

Voici une définition de la différenciation :

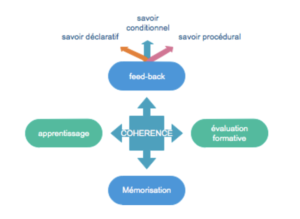
Si la différenciation est une recherche permanente de cohérence entre l’apprentissage de chaque élève et l’évaluation formative de l’enseignant,
alors il faut pouvoir observer auprès de chacun le produit et le processus de cet apprentissage par rapport à l’attendu

pour offrir un feed-back rapide qui renforce ce produit ou ce processus et qui procure des pistes d’ajustement (évaluation formative)
en vue de favoriser une mémorisation de qualité.
Ce feed-back porte sur les 3 types de savoirs : déclaratif, conditionnel et procédural.

Quels liens peut-on faire entre le « calcul’AS 3D » et la différenciation ?

Le calcul’AS 3D est un matériel de manipulation et d’observation mathématique qui a pour but le développement du sens du nombre et des opérations en sollicitant les trois types de savoirs.

Ces blocs permettent de percevoir des nombres globalisés et d’éviter le comptage par un. Ils ont une face lisse qui présente la même silhouette « force 2 » que les cartes du calcul’AS minor et une face où chaque unité est visible.

Ces blocs peuvent se poser sur une règle de mesure qui va jusque 120 et qui propose 2 « rails » : l’un segmenté par dizaine, l’autre segmenté par dizaine ET unité.

Développer le sens du nombre et des opérations,
c’est intégrer les savoirs déclaratifs mathématiques dans le schéma suivant :

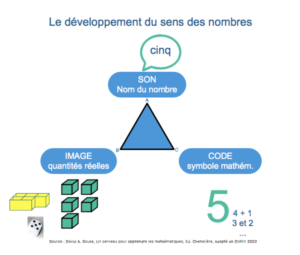
Le sens du nombre devient opérationnel lorsque l’enfant a développé (et intégré) complémentairement ces trois aspects : Le « son » du nombre, l’image du nombre et le code écrit de ce nombre.

Le travail sur ces trois éléments est fondamental et demande beaucoup d’investissement. La plupart du temps, lorsqu’un enfant rencontre des difficultés, c’est qu’il lui manque un de ces éléments. Pour certains enfants, si on leur dit « cinq », ils ne font pas d’image de ce nombre dans leur tête ou bien ne connaissent plus son code. Pour d’autres, si on leur donne le code et le son, ils n’évoquent rien ou hésitent, doivent recompter par un ou refaire une image provisoire qui s’efface après chaque manipulation. Il est donc nécessaire de proposer à ces enfants du matériel et des activités qui rétablissent ce triangle.

Pour chaque enfant, il s’agit donc d’établir une analyse de ses besoins pour re-proposer un apprentissage explicite, réparateur et porteur. S’il lui manque des images mentales, il faut lui en ré-activer avec la triple articulation. Nous sommes loin d’une différenciation pour les visuels et les auditifs et les kinestésiques qui n’a aucun sens puisque les trois sont nécessaires et indissociables.

Le matériel « calcul’AS 3D » permet une gestion mentale du nombre et des opérations. Chaque enfant est amené à imaginer et anticiper ce qu’il va se passer

si j’assemble un quatre et un trois, alors …
si j’assemble un sept et un huit, alors …
si je cherche la différence entre un 5 et un 3, alors…Comme tout « bon » matériel, il permet un étayage. Le principe d’un étayage est qu’il est amené à disparaître après avoir construit des images mentales. Une première différenciation consiste donc d’évaluer ce besoin : pour qui est-ce encore nécessaire d’utiliser le calcul’AS 3D? Cette prise en compte se fait en demandant des traces des manipulations pour observer la qualité de la mémorisation et la qualité de communication par l’usage du code.

Comment faire apparaître la nécessité du code ?

Si on demande à un enfant de faire un 5 avec des pions, il compte ses jetons un par un. Il prélève 5 jetons et les dispose, dans le meilleur des cas en formant un schème.

S’il le montre à un condisciple (image 1), ce dernier dira 5 (en comptant par un ou en globalisant) ; même si les ronds ne sont pas tous les mêmes. L’enfant n’a pas besoin d’un appui sur le code (image 2).

Que se passe-t-il avec les pièces du calcul’AS 3D?

Voici la trace d’un enfant qui a décomposé un cube 5 avec un cube 4 et un cube 1 :

Si un enfant montre la trace (image 3) à un condisciple, il peut entendre « deux » par quelqu’un ou « cinq » par un autre, si ce dernier a vu le modèle. Par contre, si on lui propose de coder, (demande résultant de l’évaluation formative basée sur la cohérence entre sa manipulation et sa trace), il n’y aura plus d’équivoque pour un tiers.

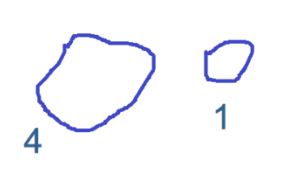
Le code devient un outil d’arbitrage et de communication. Le triangle est assuré et les trois savoirs sont sollicités :

« Un 5, c’est un quatre et un 1. » (Savoir Déclaratif),
« Pour être clair, il faut coder. » (Savoir Conditionnel),
« Je manipule, je mets en mémoire, je dessine puis je code.» (Savoir Procédural)Si l’enfant écrit « 4 et 1 », il n’a plus besoin de dessiner grâce au code. (Nouveau savoir conditionnel)
S’il veut dessiner, il est confronté à la proportionnalité. Alors, on lui propose du papier quadrillé avec l’obligation de respecter les cases unités. (Nouveau savoir procédural) Le feed-back formatif (observation et dialogue) s’aligne avec le fruit de l’apprentissage manifesté, sur les erreurs éventuelles et sur la perfectibilité possible. On comprend ainsi l’intérêt de voir les maths comme un outil de communication et donc la pertinence de l’interaction avec ses pairs avec lesquels on partage ses découvertes.

Avantage du matériel Calcul’AS 3D :

Quand on utilise des jetons, il faut chaque fois compter quand on prélève dans la boite. Par contre, grâce à la forme des nombres du Calcul’AS 3D, on le reprend dans la boite en le globalisant par sa silhouette devenue familière après de multiples manipulations antérieures. Les nombres pairs ont des formes rectangulaires, le quatre est un carré, les impairs sont des nombres pairs + 1.

Voici un défi pour stimuler la mémorisation de l’apprenant :

Mesurer des nombres avec un nombre étalon en visuel puis en agissant à l’aveugle dans un sac.

Etape 1 – Mesurer les blocs Calcul’as à partir d’un bloc 4 (en visuel). Résultats : Le bloc 5, contient un 4 et un 1. Le bloc 6, un 4 et un 2…

Etape 2 – Faire de même en cachant et manipulant les blocs dans un sac opaque puis demander :

En utilisant le 4 comme étalon, retrouvez-moi le « cinq » (sollicitation du sommet A du triangle).Comment l’as-tu reconnu ? « C’est celui qui a un en plus que le 4 ! » (évocation imagée du sommet B).
Ecris ta découverte… (sollicitation du sommet C) 4 + 1 = 5.L’évaluation formative portera sur l’expression des trois savoirs en évoquant les manipulations.
Que fais-tu pour reconnaître un 5 ? (SP)
Comment savais-tu que c’était un 5 ? (SC)
Que sais-tu du 5 ? (SD)Réponses :
SD:4et1,çafait5.
SC : Si lorsque je pose un 4 sur un bloc inconnu et qu’il y a un bloc de 1 qui dépasse, alors j’ai retrouvéle 5.
SP : Pour identifier un bloc, je prends un étalon (le 4), je le pose sur un bloc inconnu et je regarde cequi dépasse ou ce qui manque : s’il manque un, le bloc mesuré avec un 4 est un trois.
La différenciation consistera à stimuler les types de savoirs non exprimés en faisant ré-évoquer.

Autre exemple : Observer la compensation et la commutativité.

Voici un exercice similaire pour 7 + 6 (sur ta réglette éloignée puis sur ta feuille).

La différenciation portera sur le feed-back et les relances face aux productions orales et écrites de l’enfant.

Dans toutes ces activités, la mémorisation n’est pas reportée à plus tard, elle fait partie intégrante du processus stimulé pas la construction du triangle du sens du nombre et du triangle des 3 savoirs. Les activités proposées avec le matériel « Calcul’AS 3D » articulent construction cognitive, métacognition et mémorisation.