Stéphane HOEBEN
Instituteur primaire – Consultant en Education
Licence et Agrégation en Sciences de l’Education
Cet article a pour but de montrer comment un matériel bien construit INCLUT la différenciation et facilite ainsi, à la fois le travail de l’enseignant et l’apprentissage des élèves.
Afin d’être rigoureux sur le plan des contenus, voici UNE définition proposée par un groupe de chercheurs reconnus et publiée dans le rapport de la conférence de consensus de la Cnesco[1] sur la différenciation pédagogique – Comment adapter l’enseignement à la réussite de tous ? (2017)
« Le concept de différenciation pédagogique n’existe pas en tant qu’objet d’étude dans la littérature scientifique. Aussi est-il apparu nécessaire au comité d’organisation de la conférence de consensus de définir cette notion de la manière suivante :
La différenciation est la prise en compte par les acteurs du système éducatif des caractéristiques individuelles (besoins, intérêts et motivations) ; acquis, non acquis et difficultés ; modes d’apprentissage (style, rythme, pouvoir de concentration, engagement…) ; potentialités à exploiter…) de chaque élève en vue de permettre à chacun d’eux de maîtriser les objectifs fondamentaux prescrits et de développer au mieux leurs potentialités, et de permettre au système éducatif d’être à la fois plus pertinent, efficace et équitable. »
Voici également la définition proposée dans l’ouvrage « Je différencie… » [2] :
« La différenciation est une recherche permanente de cohérence entre l’apprentissage de chaque élève et l’évaluation formative (observation et dialogue) des enseignants. Cette dynamique – liée à la responsabilité de la profession – repose sur deux dimensions : éthique et méthodologique ».
Attention !
Éthique et méthodologie se supportent l’une l’autre… Ce n’est pas parce qu’on a l’âme d’un artiste que la technique n’est pas indispensable ; ce n’est pas parce qu’on applique parfaitement tous les principes techniques que l’œuvre aura une âme. Ainsi, penser que l’intérêt porté à la personnalité de chaque élève garantit son émancipation est tout aussi illusoire que de penser que l’application de conseils et de recettes méthodologiques suffit pour rencontrer vraiment l’élève. »
Il ne s’agit donc pas d’offrir une diversité ou une variété aux élèves au niveau matériel, organisation, structure… parce que c’est à la mode, et faire ainsi illusion. Il importe de s’efforcer
- d’évaluer la pertinence du matériel (ou du dispositif) en fonction des théories propres à la discipline et à la psychologie de l’apprentissage afin d’en comprendre les avantages et les dangers
- de façon formative les apprentissages des élèves au travers de mises en situations d’apprentissage.
Plus le support proposé est riche et global, comme toute réalité vécue, plus les enfants peuvent apprendre dans une visée à long terme.
Plusieurs enjeux dans l’approche des nombres sont fondamentaux et demandent une grande vigilance.
- Construire des images mentales des quantités.
- Eviter et empêcher l’apparition du réflexe du comptage.
- Favoriser la perception des nombres grâce à des décompositions.
Voir les théories de Stella Baruk et Rémi Brissiaud.
Vous trouverez donc plusieurs calcul’AS à utiliser de façon systématique et très régulière. Chacun a des limites et c’est l’ensemble qui constitue une offre optimale. Toutefois, ils ont des caractéristiques semblables au service de l’apprentissage :
- Les quantités (nombres) sont présentées de façon visuelle. Cela tient compte de ce que les logopèdes appellent le transcodage. Il est nécessaire pour l’apprenant d’aborder les nombres par 3 canaux : une image, un chiffre et un mot. C’est-à-dire le langage visuo-spatial + le langage numérique + le langage alphabétique.
- Les quantités (nombres) sont présentées de façon visuelle (une représentation) et les chiffres ne sont pas écrits à côté. En effet, cela évite que les enfants utilisent uniquement les zones de la lecture dans leur cerveau et ne construisent pas la perception d’une quantité.
- Les unités qui composent les nombres sont présentées de diverses façons structurées afin de faciliter la construction de l’image mentale du mentale par décompositions de la part des élèves.
- Les nombres sont proposés dans une version globalisée où, les unités n’étant plus visibles, les enfants se construisent une image HORS comptage par un.
- La méthodologie liée aux cartes propose des activités de découverte, des activités d’apprentissage et des activités d’entrainement (des jeux).
- La méthodologie liée aux cartes insiste que pour apprendre, il faut proposer très régulièrement des moments de métacognition afin de passer du « faire » à la logique de « penser le faire ».
Nous vous présentons brièvement 5 sortes de matériel qui concernent l’apprentissage de 4 ans à 12 ans (et + si nécessaire). Les activités avec chaque boite de cartes sont semblables et complémentaires.
1. Le calcul’AS Zador est destiné aux apprentissages des nombres jusque 6.
Il y a 4 sortes de cartes (A – B – C – D) que vous utilisez ENSEMBLE ou séparément…

Des cartes « égalité » recto-verso |
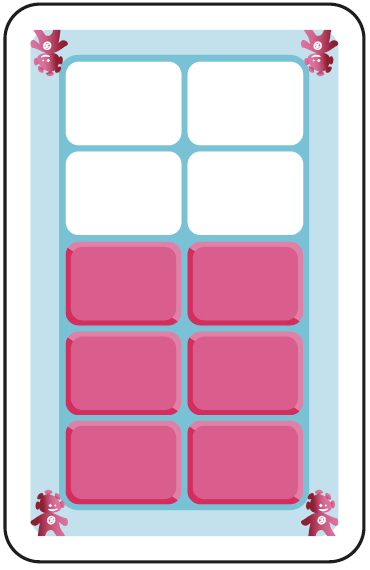
A. 6 unités visibles dans un cadre de 10 unités visibles. Nombre pair en forme de rectangle. |
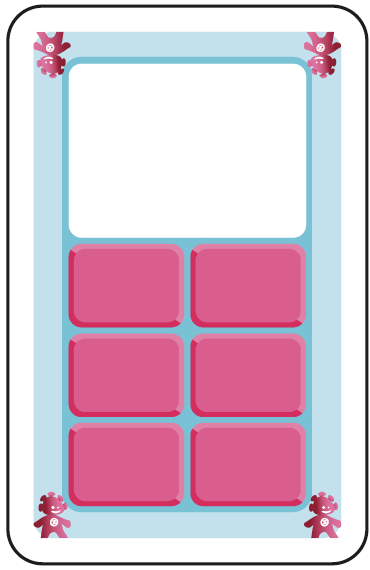
A. 6 unités visibles. Le complément de 10 est globalisé. 2 – 4 et 6 ont une forme de rectangle. |

A. 6 unités visibles sans la dizaine. Toujours le principe que le nombre pair prend une forme rectangulaire. |
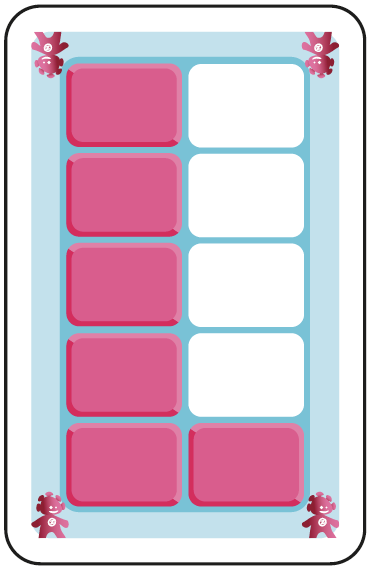
B. 6 unités visibles dans un cadre de 10 unités visibles. Les nombres sont construits sur base d’une colonne de 5. |
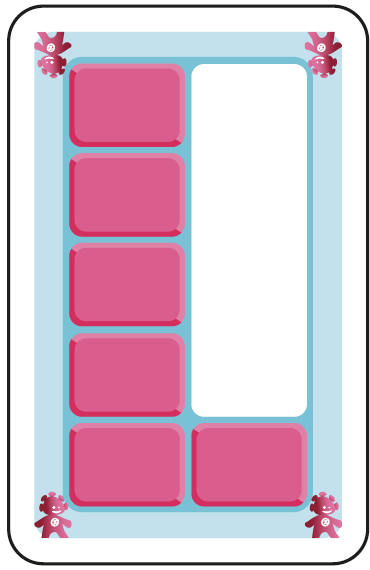
B. 6 unités visibles. Le complément de 10 est globalisé. Les nombres sont construits sur base d’une colonne de 5. |
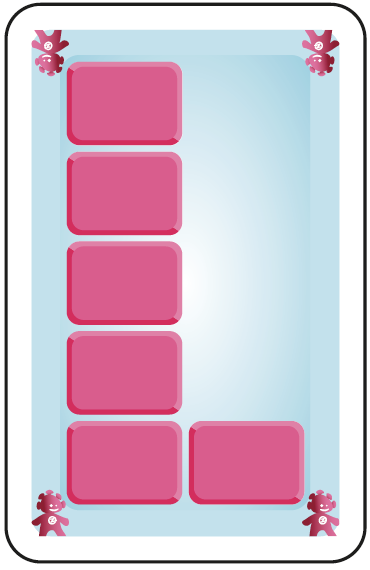
B. 6 unités visibles sans la dizaine. Les nombres sont construits sur base d’une colonne de 5. |
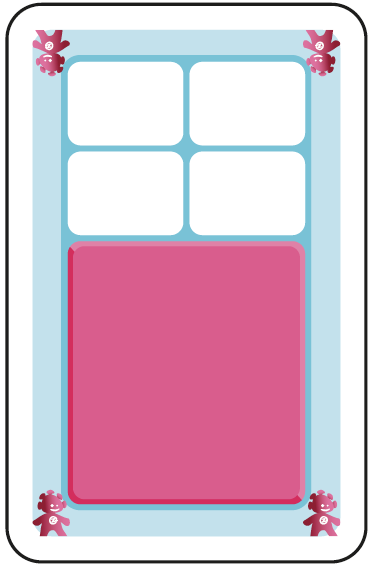
C. 6 unités globalisées dans un cadre de 10 unités. Nombre pair en forme de rectangle. |
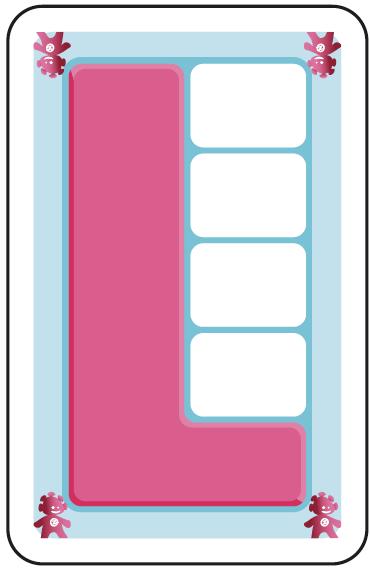
C. 6 unités globalisées dans un cadre 10 unités. Les nombres sont construits sur base d’une colonne de 5. |

D. Les nombres sont présentés avec un seul dé. |

D. Les nombres sont présentés avec deux dés. |

D. Les nombres sont présentés avec trois dés. |
Comme vous le constatez, il y a 11 variantes de cartes. La diversité des présentations ainsi que leur usage de façon isolée ou simultanée facilitent la construction des images mentales des nombres.
2. Le calcul’AS Minor est destiné aux apprentissages des nombres jusque 10 ainsi que des dixièmes.
Il y a 4 variantes de cartes « nombres » ainsi que des cartes « égalité ». Si l’équipe enseignante travaille en continuité, les enfants ont déjà rencontré ces « schèmes » en maternelles dans le calcul’AS Zador. (Il s’agit de la présentation A.) Les nombres évoluent horizontalement par des « étages » de 2 cases.
 |
Les cartes « égalité » participent à la différenciation car on peut constater que le signe « = » est très mal perçu par les enfants. En effet, il prend la signification « ça fait » ou « ça donne » au lieu de « c’est la même quantité que… » Trop souvent, lorsque les enfants manipulent du matériel dans la classe, ils n’utilisent pas ce signe pour montrer une égalité. Le signe « = » devient très vite : « Cela donne …. » ou « Cela fait ….),
|
Il est essentiel, quel que soit le matériel manipulé, de suivre cet exemple :
« 4 cases mises avec 3 cases c’est la même quantité qu’une carte de 7 cases ». ou « 4 + 2 = 6 »
Les enfants se rendent alors compte qu’une association de quantité équivaut à une quantité.
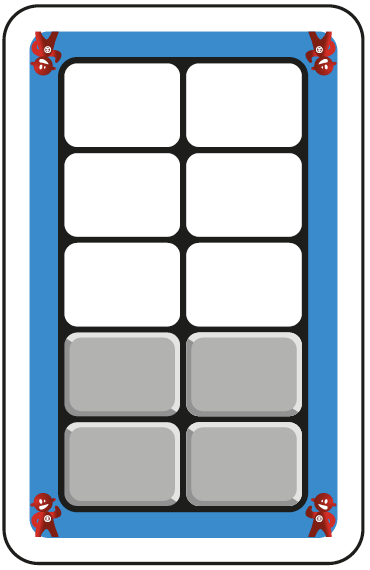
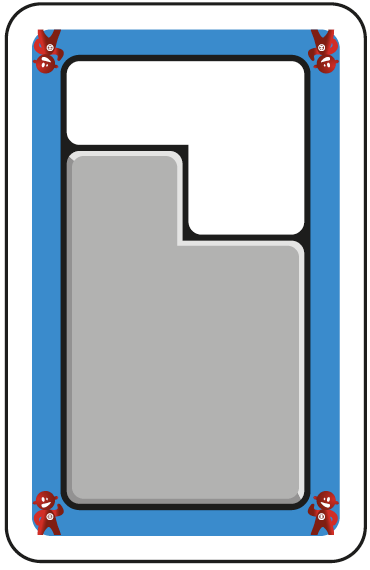

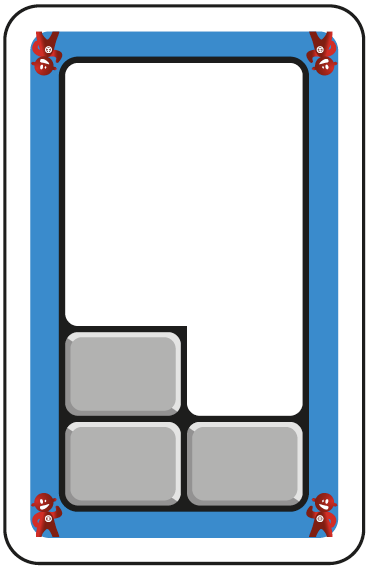
En début de scolarité, chaque case est appréhendée comme une unité et une carte « complète » vaut une dizaine. Plus tard, pour découvrir les nombres non entiers, plus précisément les dixièmes, ces cartes sont très utiles. En effet, si vous considérez que la carte vaut une unité, alors chaque case représente un dixième.
Cela permet de considérer que l’exemple illustré ci-dessus correspond à cette opération :
0,4 u + 0, 3 u = 0,7 u Beaucoup d’enfants découvrent à ce moment-là que les nombres non entiers peuvent aussi être représentés visuellement.
Les activités proposées sont indispensables pour l’apprentissage des nombres et peuvent se vivre avec beaucoup de matériel varié ET structuré !
N’oubliez pas que c’est vous qui donnez une valeur aux cases ! Soit des unités, soit des dixièmes.
- Activités de découverte
- associer les cartes de même quantité ;
- réaliser des dizaines (ou une unité) en associant deux cartes, trois cartes ;
- réaliser d’autres quantités (ex : 9, 13, 16, 20 …) avec plusieurs cartes ;
- jouer à bataille « classique » ;
- puiser au hasard 5 cartes et les placer sur une droite des nombres ;
- Activités de transcodage
Avant de « jouer » ou de s’entrainer, il est très important de solliciter plusieurs zones du cerveau pour favoriser l’apprentissage de chaque enfant ! Aussi, lorsqu’on retourne une carte, il est utile de rédiger sa carte d’identité. C’est-à-dire d’exprimer le nombre ou l’opération :- en langage numérique (nombre ou opération) ;
- en langage alphabétique (mot) ;
- en langage visuo-spatial (dessin).
Par exemple :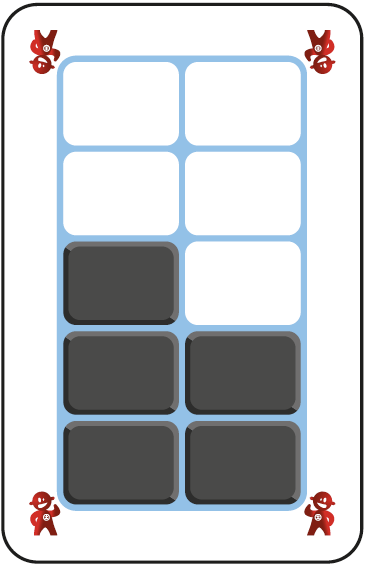
C’est 5.
Il y a cinq cases.
Je peux la représenter
ainsi : OOOOO
De même pour une addition de 2 cartes :
- Je vois une carte 2 et une carte 3
- C’est comme 2 + 3 = 5
- 2 carrés mis avec 3 carrés c’est comme une carte avec 5 carrés
- Bataille « reconnaître »
Former un paquet avec toutes les cartes. Retourner une carte. Le premier qui dit le nombre, ramasse. Après 5 ou 10 minutes de jeu, on compte les cartes.
(Il faut vivre cette activité jusqu’à ce que la reconnaissance soit automatique.) - Bataille « addition ».
A deux, se partager les cartes. Les joueurs retournent en même temps la première carte de leur paquet. Celui qui dit le plus vite la somme ramasse le pli.
Variantes :- On joue à 3 ou 4.
- On donne une valeur différente aux cases : par exemple des dixièmes.
- On donne une valeur différente aux cases : par exemple les noires sont des unités et les grisées des dixièmes.
- Bataille « soustraction ».
A deux, se partager les cartes. Les joueurs retournent en même temps la première carte de leur paquet. Celui qui dit le plus vite la différence ramasse le pli.
Variantes :- On donne une valeur différente aux cases : par exemple des dixièmes.
- On donne une valeur différente aux cases : par exemple les noires sont des unités et les grisées des dixièmes.
- Bataille « pivot ».
A deux, se partager les cartes. Les joueurs se mettent d’accord sur un nombre « pivot » : par exemple 20. Les joueurs retournent en même temps la première carte de leur paquet. Celui qui dit le plus vite la différence entre le pivot (ici 20) et la somme des deux cartes ramasse le pli.
Variantes :- On joue à 3 ou 4.
- On donne une valeur différente aux cases : par exemple des dixièmes.
- On donne une valeur différente aux cases : par exemple les noires sont des unités et les grisées des dixièmes.
- Bataille « multiplication ».
- Bataille « diviseur ».
3. Le calcul’AS Trezor est destiné aux apprentissages des nombres jusque 10 ainsi que des dixièmes.
Comme les cartes précédentes, il y a 4 variantes de cartes « nombres » ainsi que des cartes « égalité ». La disposition est cependant différente puisque les nombres sont présentés dans une structure verticale de 2 colonnes de 5 cases. La dizaine se construit donc comme 2 colonnes de 5.
Si l’équipe enseignante travaille en continuité, les enfants ont déjà rencontré ces « schèmes » en maternelles dans le calcul’AS Zador. (Il s’agit de la présentation B.)
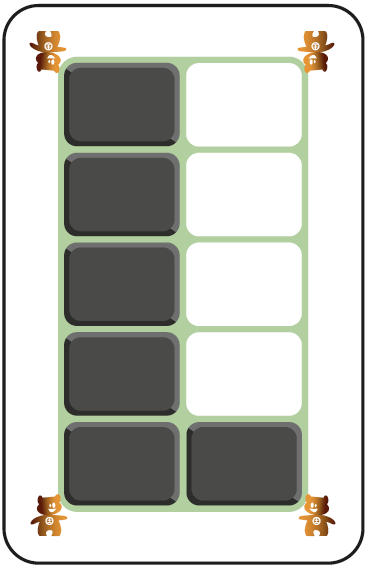
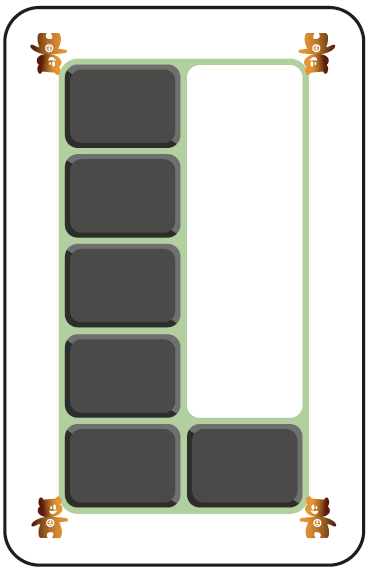
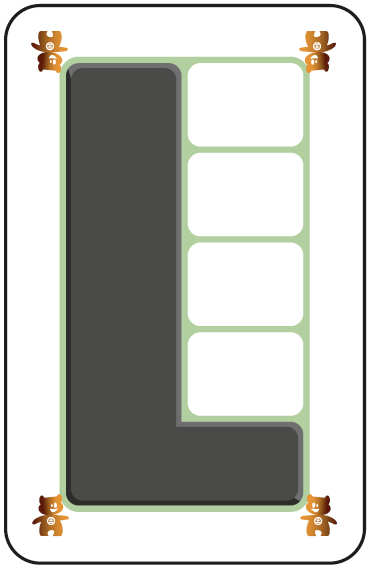

Certains enseignants préfèrent les cartes bleues ou les cartes vertes. Cela montre toute la dimension personnelle dans la perception visuelle des schèmes. Pour apprendre, il ne faut surtout pas s’enfermer dans un matériel qui est trop familier. Pour élargir son horizon de connaissances, il est indispensable de rencontrer un maximum de représentations structurées des nombres et d’avoir le temps de les intégrer.
4. Le calcul’AS Major est destiné aux apprentissages des nombres jusque 100 ainsi que des dixièmes et les centièmes.
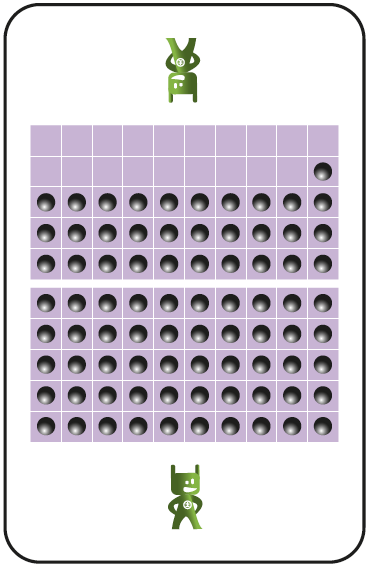
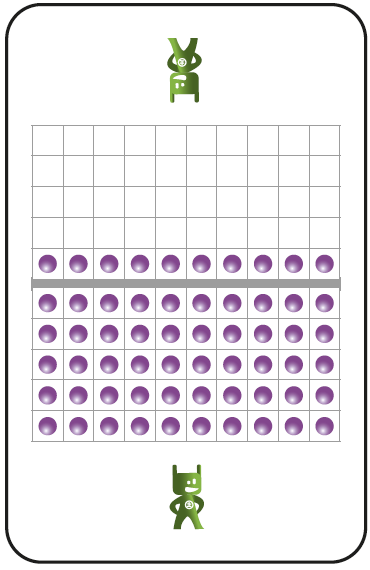
Les cartes sont réalisées sur base d’un carré de 10 sur 10 (soit 100). La séparation permet de voir rapidement si on est au-dessus ou en dessous de 50. Si on considère un carré complet comme une unité, alors on travaille avec des centièmes. La position du personnage « Major » donne également un repère visuel de la moitié de la ligne.
Les deux séries permettent de proposer – à partir de la 4e ou 5e année – que les « billes noires » des cartes soient considérées comme des unités et les « billes roses » comme des dixièmes ou des centièmes.
 |
 |
Comme dans l’article précédent de Bernard Kersten, à propos du Calcul’AS 3D, il est important pour la différenciation de travailler le + souvent possible en logique de transcodage.
|
Avant de « jouer » ou de s’entrainer, il est très important de solliciter plusieurs zones du cerveau pour favoriser l’apprentissage de chaque enfant ! Aussi, lorsqu’on retourne une carte, il est utile de rédiger sa carte d’identité. C’est-à-dire d’exprimer le nombre ou l’opération :
- en langage numérique (nombre ou opération)
- en langage alphabétique (mot)
- en langage visuo-spatial (dessin)
Par exemple :
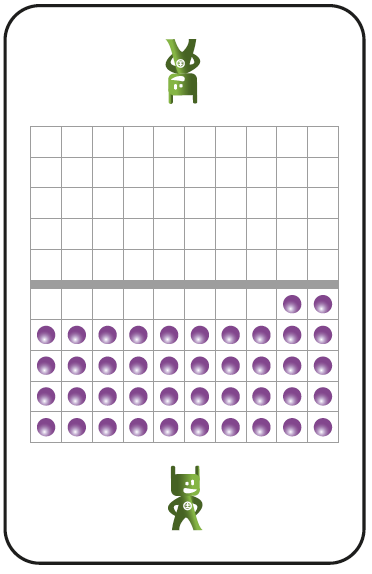 |
C’est 42.
Il y a quarante-deux points. Je peux la représenter Comme 4 dizaines et 2 unités. |
De même pour une addition de 2 cartes :
·Je vois une carte 17 et une carte 35 c’est comme 52 billes ensemble. |
| ou,
si les billes valent des dixièmes : C’est 4,2 unités 4 unités et 2 dixièmes |
ou,
si les billes valent des centièmes : C’est 0,42 unités 42 centièmes |
5. Le calcul’AS Yééh !
Il a été créé suite à la demande de logopèdes de disposer d’un support de cartes transparent afin de superposer des cartes-nombres ET voir apparaitre des différences entre les nombres. Il est également possible d’associer des cartes pour illustrer des additions et voir la somme.
Les cartes sont en outre construites selon diverses décompositions : par 1, par 2, par 3 et par 4. Cela permet d’exprimer que le nombre 6 peut être décrit comme 1 + 1 + 1 + 1 + 1 + 1. Que 6 = 2 + 2 + 2 . Que 6 = 2 + 4. Que 6 = 3 + 2+ 1. Que 6 = 3 + 3. …..
[1] Cnesco (2017) Différenciation pédagogique : comment adapter l’enseignement à la réussite de tous les élèves ? Dossier de synthèse. http:/www.cnesco.fr/fr/differenciation-pedagogique/
[2] HOEBEN S. & LEROY P-M., Je différencie pour mieux tenir compte des écarts entre élèves. (2020) Sambreville : Editions Atzéo.














